皆さん、こんにちは。

先日（2021年12月11日）の読売新聞の夕刊の「よみうり寸評」にとても気になる記事がありました。

「学校のクラスに誕生日が同じ子はいるか。直観的には『そうそういるものではない』と思うが、これは確率の問題なので答えは計算できる。クラスの規模が大きくなるにつれ、誕生日が同じ子がいる可能性はどんどん高まる。1学級23人の時点で確率は50％を超え、30人で約70％、40人で約90％となる。意外な結果のため『誕生日のパラドックス』と呼ばれる。」

筆者と同じく私の直観も確かに「そうそういるものではない」ですし、確率の問題としての計算は、「一人の人が自分と同じ確率は365分の1なので、40人学級では40/365で10％ちょっと」ではないかというのが私の考えでした。

しかし、記事にもあるように実際には40人で約90％となり、これを「誕生日のパラドックス」と呼ぶとのこと。

記事にはそれ以上の説明はなく、どうしようもなく気になってしまいすぐにネットで調べてみました。

その結果、こんなサイトを見つけましたが数式がちょっと難しかったのでそこからもう少し分かりやすく算数のレベルで考えなおしてみます。

まず次の二つを考えます。

（1）ある集団の中に、同じ誕生日の人がいる確率（2）ある集団の中で、どの人も誕生日が別である確率（1）と（2）を足すと1（100％）ですので、（2）をまず計算して1から引けば（1）の確率になるはずです。

具体的にみますと、2人の集団の場合、2人目が最初の人と違う誕生日の日付は364通りありますので、

1-（364/365）＝0.3％となり、

3人の集団の場合、1-（364/365×363/365）＝0.8％となります。

このように、一人増えるごとに分子の数を一人ずつ減らした確率をどんどんかけていけばよいのです。

そうです、実は私たちの直観とは、「クラスの生徒の誕生日が重なり合わず皆違う」ということを前提の計算に基づいていたということです。

そんなことになる確率は限りなく少ないということを理解していれば、この直観はかなり現実のものに近くなったはずです。

ちなみにこのサイトによると、「クラスの中で自分と同じ誕生日の子がいる確率」というのは逆に365人なんていうマンモス学級があった仮定したとしても、下のグラフのように60％程度にしかならないようです。

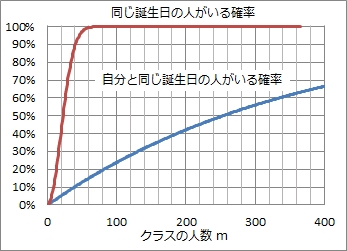
まあ、収益率30％のギャンブルに三回かけても元が確実に取れるとは限らないということと同じですね。

このことを知ると、世の中には「誕生日のパラドックス」に限らず「〇〇のパラドックス」は数限りなくありそうな気がしてきます。